1 min to read
Challenges - Calculus - 200827
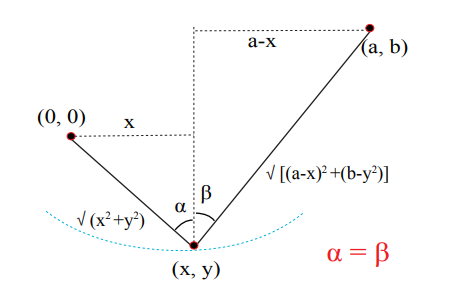
Constraint: The length L of the string is fixed.
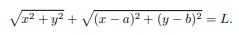
The function y = y(x) is determined implicitly by the constraint equation above. We traced the constraint curve (possible positions of the ring) on the blackboard; the curve is also suggested in blue in Figure 1. This curve is an ellipse with foci 1 at (0, 0) and (a, b), but knowing that the curve is an ellipse does not help us find the lowest point.
Experiments with the hanging ring show that the lowest point is somewhere between x = 0 and x = a. (This is one way we can confirm that the minimum solution isn’t at one of the ends of the string; don’t try to use the second derivative test.) Since the ends of the constraint curve are higher than the middle, the lowest point is a critical point (a point where y’(x) = 0).
To find the critical point, differentiate the constraint equation implicitly with respect to x:
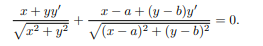
Since y’ = 0 at the critical point, the equation can be rewritten as:
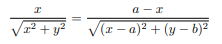
From the figure at the beginning of the answer, we see that the last equation can be interpreted geometrically as saying that:
sin α = sin β ⇒ α = β
where α and β are the angles the left and right portions of the string make with the vertical.
And that is the condition we want for the question. If you want to find out what the exact value of x and y, you can add some other steps.



Comments