1 min to read
The Hanging Cable
 Solution
Solution
First question: the center of the cable is 10m above the ground
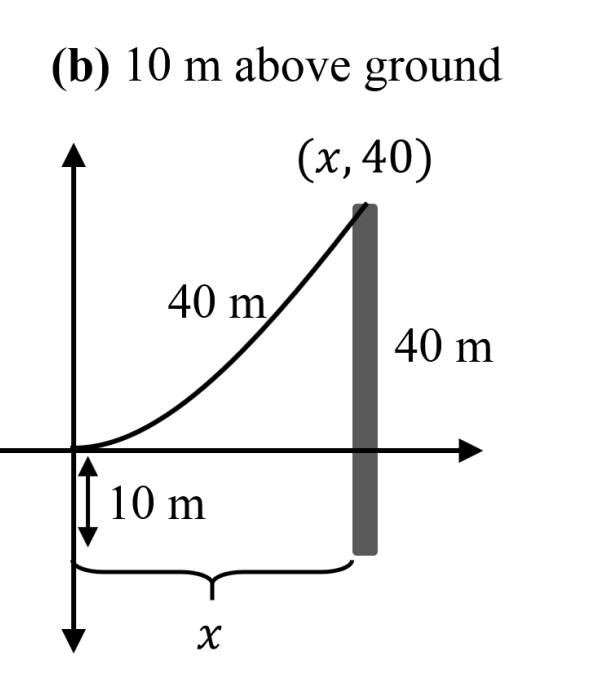
Using just half of the picture for simplicity, you can easily notice that:
If the cable is 80 m, then half of it is 40 m. But notice 40 m from the top of a 50 m pole is already 10 m above the ground. The cable therefore is hanging directly downward! The cable has to be doubled back upon itself, and the two poles must be coincident and 0 m apart!
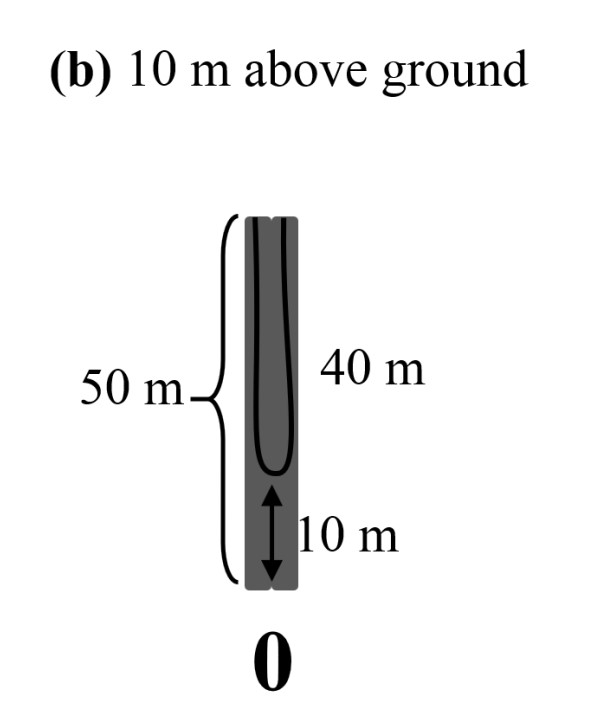
This part is actually a trick question: the two poles are a distance of 0 apart. No physics was required to solve this one, just logical thinking!
Second question: the center of the cable is 20m above the ground
The equation for a catenary tangent/touching the ground/x-axis is: y = a cosh(x/a) – a
The arc length can be written as: a sinh(x/a)
The parameter a is unknown, and we want to solve for the value of x of the pole.
Note the top of the pole is (x, 30), so we get one equation:
a cosh(x/a) = 30 + a
We also know that half of the cable length is 40 m, so using the equation for arc length of a catenary, we get another equation:
a sinh(x/a) = 40
We divide both equations by a to get:
cosh(x/a) = (30 + a)/a
sinh(x/a) = 40/a
We then use the hyperbolic identity:
cosh2 t – sinh2 t = 1
Substituting, we get:
(30 + a)2/a2 – (40/a)2 = 1
We can solve this to get:
a = 35/3
Then we use the equation:
(35/3) sinh (x/(35/3)) = 40
x = (35/3) arcsinh(120/35)
x = (35/3) ln(120/35 + √((120/35)2 + 1)) ≈ 22.7
As this is half the hanging chain, the distance between the two poles is then double this value:
2x = (70/3) ln(7) ≈ 45.4 m
Did you get the right answer?



Comments