10 min to read

Statistics - Descriptive Statistics - Visualization

Featured image

This article is a part of the Statistics - 101 series, you can access the full version of the series here:

Welcome to the third article of the Statistics 101 series. In the last article, you have learnt how to summarize data using numbers.

But “a picture is worth a thousand words”, right? Visualization is an integral part in a Data Scientist toolbox, not only because of its effect on human’s perspective (some people prefer graphs and charts to numbers), but it can also yield useful information that is hidden behind numerical figures.

After reading this article, you will learn:

1. Overview

1.1. Why do we even need visualization?

As mentioned before, visualization plays a very crucial part in every data project. To better understand its importance, refer to the example below:

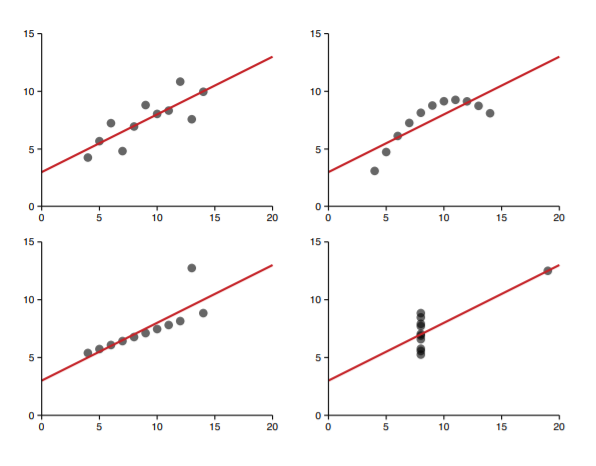
Can you guess what happened here? This is a famous exercise by Francis Anscombe (1973).

The graphs are illustrated by using 4 different datasets which all have identical linear statistics: mean, variance, correlation, even the regression line are identical. By looking at only numerical summary statistics to determine the true nature of the data can result in misleading result, which can be avoided if visualization is implemented.

For example, the top right dataset would be better represented by a polynomial regression function, not linear as described in the graph. Or the point at (20,13) in the bottom right corner can almost be surely classified as an outlier, and should be remove from the analysis.

Such information is not apparent without directly seeing what the data would be in graphs and charts. And that’s when data visualization comes in handy, it supplements the information we gathered from summary figures.

1.2. Types of visualization

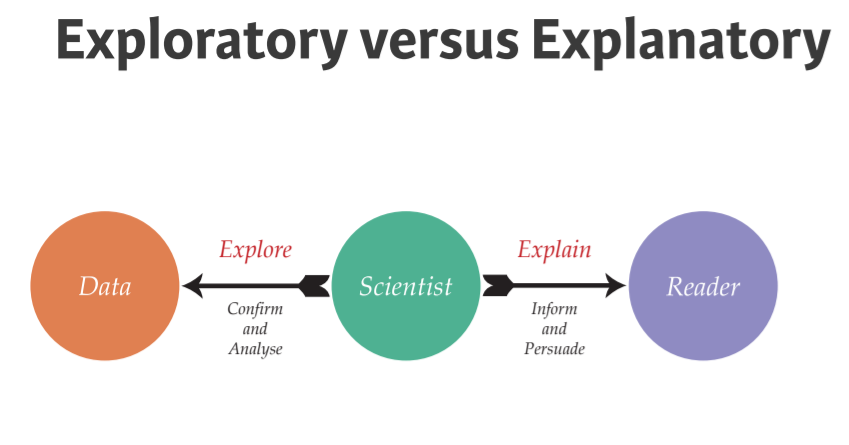
When you access the visualization universe, there are two types of visualization, each comes with very different target and process.

1.3. The grammar of visualization

Before we dive into different types of plot, first you need to equip yourself with the vocabulary in the visualization universe.

Element Description Example
Data The dataset being plotted iris dataset
Aesthetics The scale onto which we map our data x, y
Geometries The visual elements used for our data points, lines, areas
Facets Plotting small multiples dividing into smaller plots on different flower types
Statistics Representation of the data to aid understanding linear regression line, confidence interval
Coordinates The space on which the data will be plotted zooming, flipping
Themes All non-data ink fonts, axis ticks

2. Types of plots

2.1. Proportion

2.1.1. Pie chart

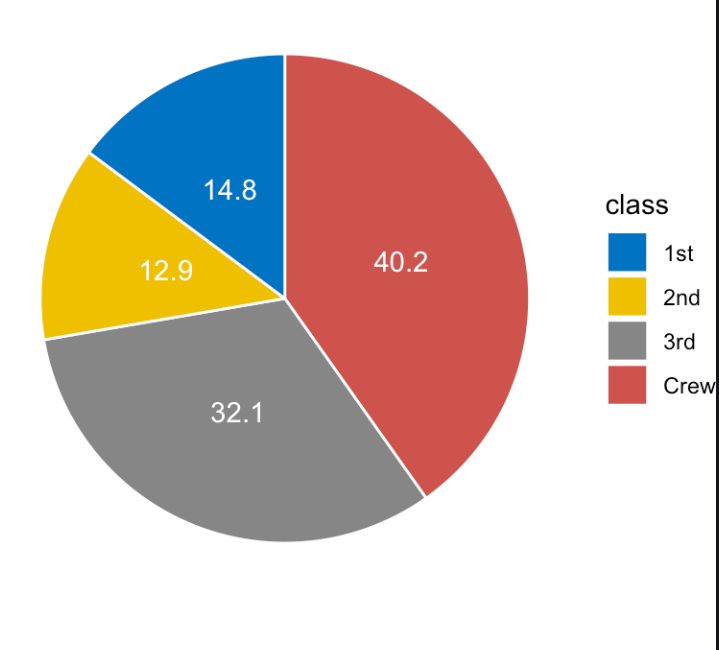
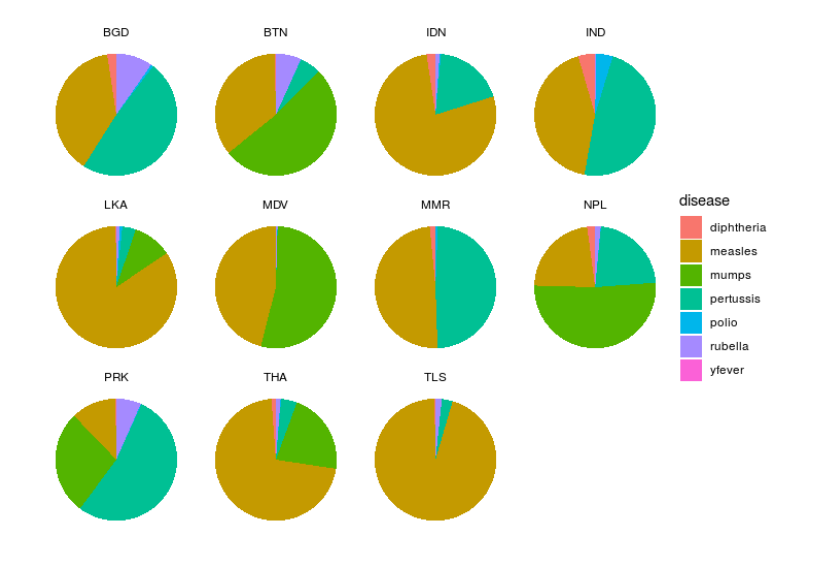
Advantage:

Disadvantage:

2.1.2. Waffle chart

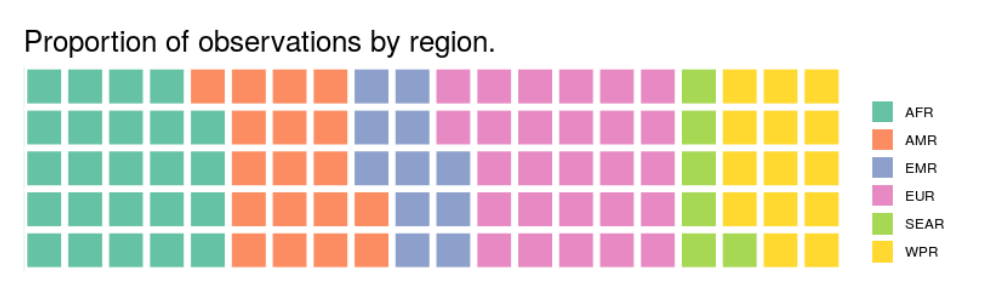
Taken into account these weakness of pie chart, waffle chart is born to tackle these. By dividing the space into 100 equal squares, each stands for 1%, you can easily compare the proportions of classes within one chart by counting how many squares a class occupies. However, comparing among several class is still a pain since the problem of no anchoring points still linger in this type of plot.

Advantage:

Disadvantage:

2.1.3. Stacked bar

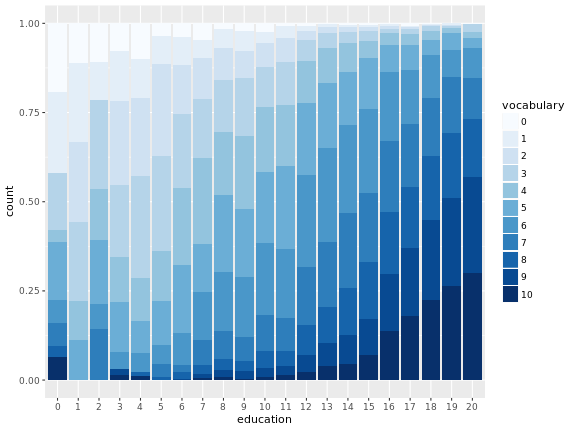
If pie and waffle chart both cannot resolve the problem of comparing multiple proportion, stacked bar is born with the view to achieve that goal.

By presenting each proportion as a single column and combine multiple columns together, stacked bar efficiently allow us to visually compare the value of a class among multiple proportion.

Advantage:

Disadvantage:

2.2. Point

2.2.1. Bar chart

One of the most popular chart used to represent data point is bar chart. Bar chart is used when a categorical value is mapped to one of the axis

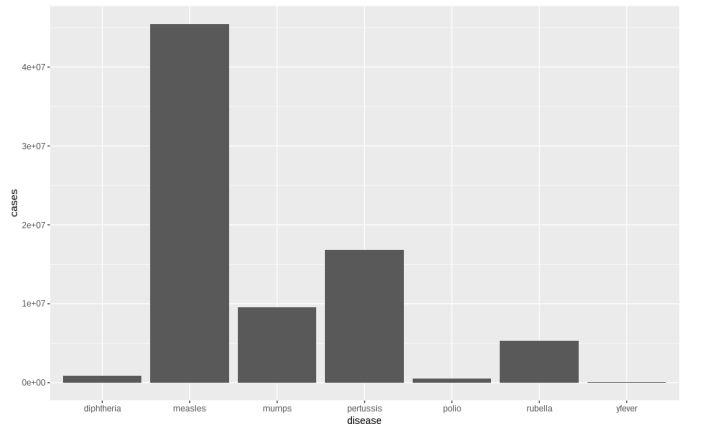
Advantage:

Disadvantage:

2.2.2. Point chart

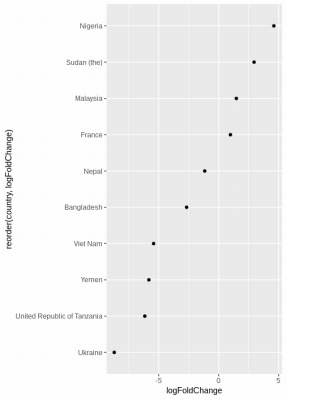
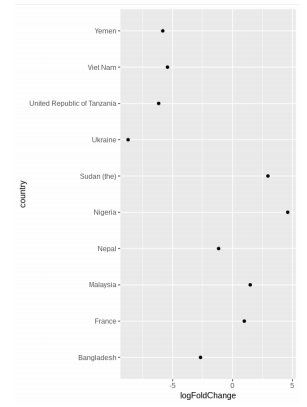
Point chart is an alternative to bar chart, fixing the problem of requiring large space. To increase the interpretability of the chart, the result should be sorted as in the above figure.

Advantage:

Disadvantage:

2.3. Distribution

2.3.1. Histogram

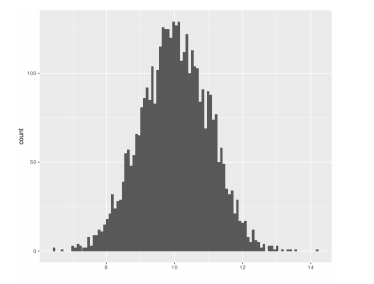
A histogram is an approximate representation of the distribution of numerical data.

To construct a histogram, the first step is to “bin” (or “bucket”) the range of values—that is, divide the entire range of values into a series of intervals—and then count how many values fall into each interval.

Choosing an appropriate numbers of bins in a histogram is a work that require great data sense and patience too. Too few bins can lead to a graph that looks like a bar code (as in the following chart), and too many would hide useful insights from the data.

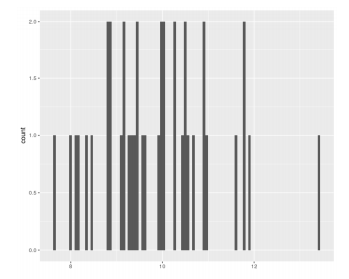
Advantage:

Disadvantage:

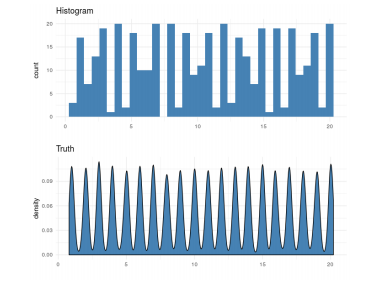
2.3.2. Kernel Density Plot

To avoid data spike as stated in the previous part, Kernel Density Plot (KDE) is usually adopted.

In KDE plot, each data point is considered as a normal distribution with equal binwidth, the overlapping part is then summed up to finalize the plot

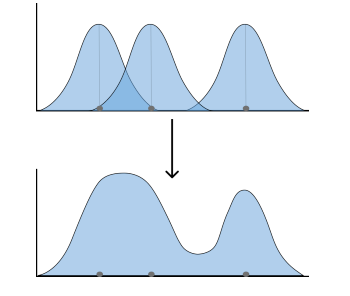
Advantage:

Disadvantage:

2.3.3. Kernel Density Plot together with rug plot

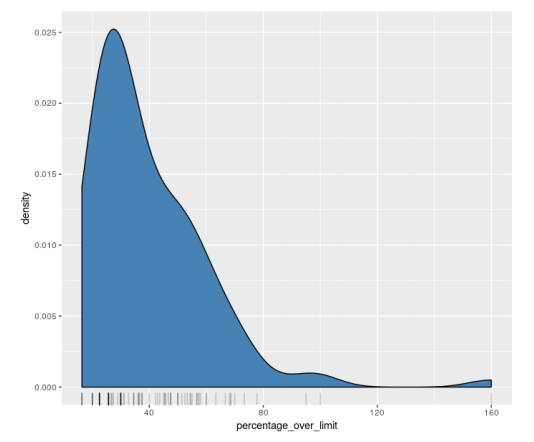
Using such method to smooth out the distribution of a numerical data, some insight could be hidden in KDE plot. As a best practice, use KDE plot together with rug plot to fully extract information from the dataset.

Rug plot is usually located under the KDE plot, each data point would be represented by a black line. The darker the area, the more data points are located in such area.

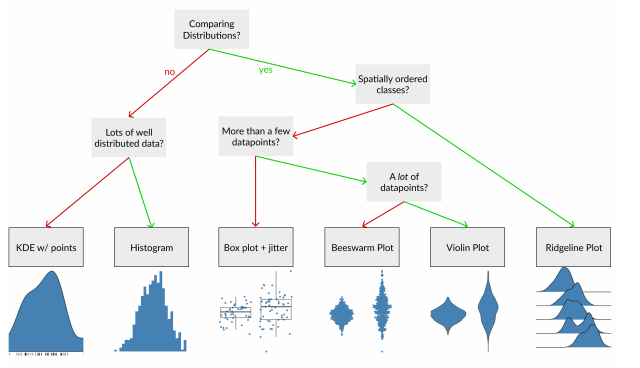
2.4. Comparing distribution

2.4.1. Boxplot

We know that we can use histogram or KDE plot to demonstrate a distribution, but such charts are not effective when being used to compare different distribution since they cannot be stacked together for comparison.

In such case, the most popular chart is boxplot, since it can contain a lot of information: where most of the data is located (median, 25% percentile, 75% percentile, whisker) and potential outliers. If you forgot about IQR, refer to the last article.

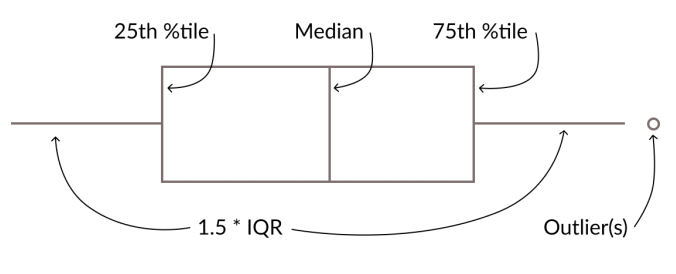
However, using boxplot alone can create a confusing result, since all the measures used (median, 25% percentile, 75% percentile) are constructed using only the relative position of such value in the dataset, which means that these measure do not take into account the actual value of other data points. As a result, two similar boxplot can have very different underlying data, as shown here:

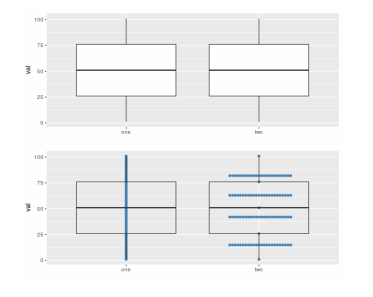
As a result, using boxplot, together with a scatterplot (jittered) would yield more information and a more accurate conclusion. However, there is a downside for this, which will be discussed in the next section.

Advantage:

Disadvantage:

2.4.2. Beeswarm

Using boxplot and scatterplot simultaneously is very useful, most of the cases. But there should there be a medium to large amount of data, it would create even more confusion.

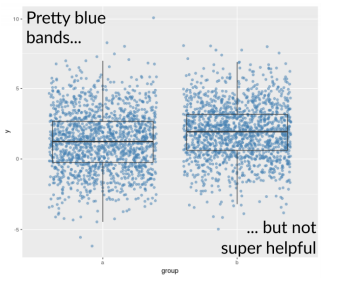
That’s when plots like beeswarm and violin come in handy. While a box plot only shows summary statistics such as mean/median and interquartile ranges, the violin plot shows the full distribution of the data

Beeswarm plot is built on the basis of scatterplot and histogram. In beeswarm plot, every data point is shown, and packed next to each other. Individual point are clumped together as close to the axis as possible but not allowed to be overlapped (this is called smart jittering).

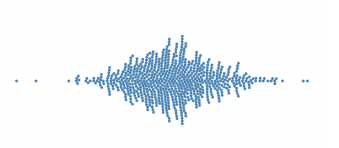
Advantage:

Disadvantage:

2.4.3. Violin

Remember that beeswarm is somewhat the combination of scatterplot and histogram? And histogram has a problem that should be fixed by KDE plot?

The notion is the same for beeswarm plot and violin plot.

Advantage:

Disadvantage:

2.4.4. Ridgeline

Ridgeline plot is a special plot used to compare distribution. It is specifically used for ordinal data. In Ridgeline plot, one ordered dimension is mapped onto one of the axis, which is useful for comparison.

Ridgeline plot adopted KDE, as a result, it bears pretty much every advantage and disadvantage of KDE plot.

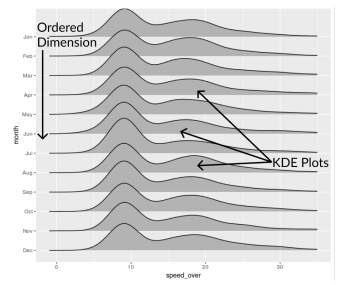
Advantage:

Disadvantage:

3. Wrap up